The potential is finite everywhere, so the wavefunction and its derivative must both be continuous everywhere. Also, the wavefunction must be normalizable, so it must go to
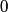 as as  goes to positive and negative infinity. Also, because we are told that the wavefunction represents a bound state, the total energy must be less than the value of the potential outside of the well, which is goes to positive and negative infinity. Also, because we are told that the wavefunction represents a bound state, the total energy must be less than the value of the potential outside of the well, which is  . This implies that that wavefunction is a decaying exponential outside of the well. The only option that satisfies all of these requirements is (B), therefore this is the correct answer. . This implies that that wavefunction is a decaying exponential outside of the well. The only option that satisfies all of these requirements is (B), therefore this is the correct answer. |